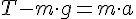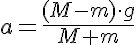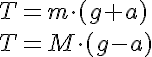5.2 Plano vertical

El problema del ascensor

Imagina que estás en un ascensor encima de una báscula. Obviamente, cuando el ascensor está en reposo, lo que marca la báscula es tu peso. En realidad, tú haces sobre la báscula una fuerza igual a tu peso (P), que ella te devuelve por reacción (N, normal, que es lo que marca la báscula), por lo que la resultante que actúa sobre ti es nula.

Pero ¿qué sucederá cuando el ascensor sube o baja con velocidad constante? ¿Y con aceleración constante? ¿Qué marcará la báscula en cada caso? Para saberlo, utiliza el simulador siguiente.

En resumen, puedes utilizar la ecuación siguiente, que sirve para todos los casos, teniendo en cuenta, como siempre, signo positivo hacia arriba:

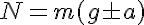
Icono IDevice Actividad de Lectura

Un sistema de dos cuerpos

En este simulador la fuerza no la realiza un dinamómetro, sino que hay dos cuerpos enlazados -el taco y el portapesas-, de forma que uno de ellos cuelga (m2) y su peso (m2g) es la fuerza de arrastre sobre los dos cuerpos (m1+m2). Por tanto, la ley fundamental se puede expresar como:

m2g=(m1+m2)a


a) ¿Es proporcional la aceleración a la masa del portapesas?

b) ¿Qué aceleración llevará el sistema cuando el portapesas tiene una masa de 200 g y el taco de 600 g? Debes obtener el resultado aplicando el segundo principio, y comprobarlo con el simulador.

c) ¿Cómo es y cuánto vale la aceleración si las masas son iguales? Demuéstralo matemáticamente.

d) Indica dos formas de conseguir que el sistema se mueva con aceleración de 3 m/s2. Utiliza el simulador y haz después la demostración matemática.




La máquina de Atwood
 
Dentro del conjunto de sistemas dinámicos formados por cuerpos enlazados, otro caso de particular interés es el de una máquina simple: la polea, que nos permite elevar un cuerpo más fácilmente al poder aplicar la fuerza hacia abajo.
 
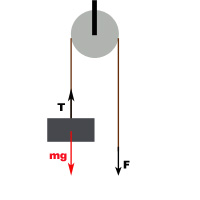La polea más sencilla es la polea simple, que transmite directamente la fuerza realizada sobre la cuerda hasta el cuerpo, tal y como se indica en el diagrama adjunto. Resulta evidente que, en este caso T = F .
 
Realmente, éste es un caso de un único cuerpo, pero existe una variante de la polea simple que resulta ser el caso más simple de cuerpos enlazados en movimiento vertical. Es la conocida como máquina de Atwood, y se trata básicamente de una polea simple en la que en el otro extremo de la cuerda se ubica otro cuerpo.
 
De nuevo la cuerda no tiene masa, es inextensible y no existe rozamiento de ningún tipo entre la polea y la cuerda.
Icono de iDevice Ejemplo o ejercicio resuelto

La máquina de Atwood (I)

Es una máquina simple de primera especie cuyo esquema se indica en la figura.

a) Escribe las ecuaciones del movimiento del sistema.

b) ¿Cuál será el valor de la aceleración?

c) ¿Cuánto vale la tensión de la cuerda?

 

 


Icono de IDevice de pregunta AV - Pregunta de Elección Múltiple

La máquina de Atwood (II)

Tienes una máquina de Atwood en la que las masas de los cuerpos son m = 2 kg y M = 8 kg.

¿Qué aceleración experimentará el sistema al dejarlo en libertad?

       
10,25 m/s2
11,76 m/s2
5,88 m/s2

¿Cuál será la tensión de la cuerda?
       
28,56 N
31,36 N
20,45 N

Icono IDevice Actividad de Lectura

Con la máquina de Atwood

Realiza una distribución de masas en la máquina de Atwood para que se mueva con una aceleración de 5 m/s2 hacia la derecha. Demuestra analíticamente el resultado obtenido.




« Anterior | Siguiente »