4.2 Plano horizontal con rozamiento
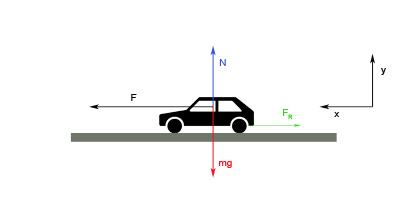
Ahora vas a estudiar un caso un poco más complicado del problema anterior; en él añadirás la existencia de una fuerza de rozamiento, caracterizada como ya has visto por un coeficiente de rozamiento μ. La diferencia consiste en la presencia de una nueva fuerza de rozamiento FR en sentido contrario al movimiento, según se indica en el siguiente esquema:
 |
La única consideración que debe hacerse es que su valor depende directamente del de la fuerza Normal, por lo que se produce una interdependencia entre las ecuaciones de los distintos ejes. Así pues, para resolver los problemas de rozamiento será necesario realizar los cálculos para ambos ejes.
Fíjate en cómo quedan las ecuaciones para este caso general de movimiento horizontal con rozamiento:
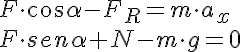
Teniendo en cuenta que el valor de la fuerza de rozamiento es FR = μ·N, puede escribirse:
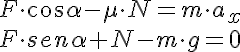
Con este sistema de ecuaciones puedes resolver cualquier problema de movimiento horizontal, añadiendo más fuerzas si fuera necesario, asegurándote de incluirlas con su dirección y signo correctos.
¿Qué coeficiente de rozamiento se utiliza?
En los problemas con rozamiento debes recordar siempre que existen dos tipos de coeficiente de rozamiento (μ), y utilizar uno u otro en función del caso que tengas que resolver:
- Si el cuerpo no ha comenzado a moverse o quieres calcular en qué momento comienza a hacerlo utilizarás el coeficiente de rozamiento estático (μes).
-
Si el cuerpo ya se encuentra en movimiento, utilizarás el coeficiente de rozamiento dinámico (μdi).
En coche
 |
Sobre asfalto mojado
Cuando el asfalto está mojado, el coeficiente de rozamiento disminuye drásticamente hasta valores tan bajos como μes = 0,3 y μdi = 0,25 respectivamente. ¿Cómo variarán las fuerzas necesarias respecto a las calculadas en el apartado anterior? ¿Será esto positivo a la hora de la conducción del automóvil?