3.2 Resolución de problemas
- Las ecuaciones se aplican a cada movimiento por separado y debes tener cuidado en diferenciar entre las variables de un movimiento y otro. Esto puedes conseguirlo añadiendo subíndices que las identifiquen.
- Aunque algunas variables sean diferentes para los dos movimientos, otras serán iguales. Deberás identificar primero estas últimas, pues te permitirán reducir el número de variables en el problema y hacer la solución mucho más fácil.
- En el caso en que algún movimiento sea la continuación de un primero, entonces la velocidad final y la posición final del primero serán la velocidad inicial y la posición inicial del segundo.
- Muchas veces la resolución gráfica de este tipo de problemas, representando en la misma gráfica los movimientos de todos ellos, permite una solución más rápida de los mismos.
Pre-conocimiento
 |
El perro y el cazador
Un cazador y su perro vuelven de cazar, desplazándose ambos con velocidad constante. El cazador anda a 5 km/h, mientras que el perro se desplaza a 8 km/h. El perro no puede parar quieto y se mueve realizando viajes de ida y vuelta de la posición de su dueño a casa y así continuamente.
Si cuando comenzaron el retorno estaban a 10 km de la casa, ¿cuál será la distancia total recorrida por el perro?
Aunque aparentemente se trate de un problema de dos cuerpos, de complicada resolución, la respuesta es sorprendentemente sencilla.
El cazador tardará 2 horas en llegar a su casa, ya que en cada hora
recorre 5 km y se encontraba a 10 km de ella. Pero dado que el perro se
mueve con velocidad uniforme de 8 km/h durante el mismo tiempo y no se
detiene en ningún momento, en esas dos horas recorrerá 16 km. ¡Obvio!
Ejemplo o ejercicio resuelto
El auto móvil
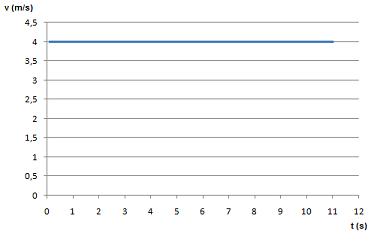
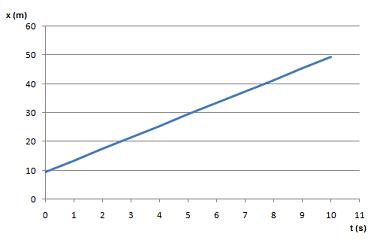
Un automóvil recorre una recta con velocidad constante. En los instantes t1 = 0 s y t2 = 5 s, sus posiciones son x1 = 9,5 m y x2 = 29,5 m.
 |
A partir de estos datos, determina:
Ejemplo o ejercicio resuelto
 |
Te adelanta una moto
Si cuando vas en tu coche a 100 km/h te adelanta una moto que se mueve a 120 km/h ¿con qué velocidad se va alejando de ti? ¿A qué distancia se encuentra la moto que te ha adelantado media hora después si las velocidades no cambian?
AV - Pregunta Verdadero-FalsoLa planta embotelladora
En una planta embotelladora de agua existe una cinta transportadora en la que una botella pasa por delante del empleado cada 20 segundos. Si la distancia entre botellas consecutivas es de 40 cm, indica si son verdaderas o falsas las siguientes afirmaciones:
Verdadero Falso
Verdadero Falso
Verdadero Falso
Ejemplo o ejercicio resuelto
 |
¿Qué velocidad lleva?
Observa la imagen. Circulando por una carretera a 108 km/h llevas por delante un coche que también se mueve a velocidad constante. Cuando está a aproximadamente 150 m por delante comienzas a medir el tiempo que te cuesta adelantarlo, que resulta ser de un minuto. Haz una estimación de la velocidad que lleva el coche que has adelantado.
AV - Reflexión
Autos locos
Fíjate en la gráfica siguiente. Compara cualitativamente el movimiento de los tres "autos locos" y escribe las ecuaciones correspondientes a cada uno de ellos.
 |
Ejemplo o ejercicio resuelto
Dos móviles
Dos ciudades A y B están separadas por 420 km. De la ciudad A sale una motocicleta a las doce del mediodía en dirección a B con velocidad constante de 80 km/h. Dos horas después sale de B un automóvil con dirección a A, siendo su velocidad uniforme de 120 km/h.
 |