2.1 Cambios de energía
Ya has visto que existe una relación entre el trabajo y la energía. De hecho, el trabajo es una forma de transferir energía de un cuerpo a otro.
Así, si realizas un trabajo sobre un cuerpo, por ejemplo al empujar una caja sobre un plano horizontal, ese trabajo se invierte en aumentar la energía cinética de la caja, que se mueve a mayor velocidad.
¿Y si subes la caja verticalmente a velocidad constante? Entonces aumentas su energía potencial.
Si es el cuerpo el que realiza el trabajo, está transfiriendo energía a otro cuerpo. Piensa en dos patinadores y en cómo varían su energía cinética cuando chocan: un patinador disminuye su velocidad y el otro la aumenta.
|
Trabajo y energía potencial
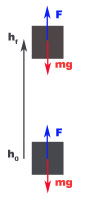
Si sobre un cuerpo de masa m aplicas una fuerza igual a su peso dirigida verticalmente hacia arriba entonces lo haces subir a velocidad constante (¡como la fuerza total es nula, la aceleración también lo será!). Si su altura se incrementa en h metros, desde una altura inicial ho a una altura final hf, el trabajo realizado será:
W = F d = mgΔh = mg(hf - ho) = mghf - mgho= Ep,f - Ep,o = ΔEp
Es decir, el trabajo realizado por una fuerza sobre el cuerpo es igual a la variación de la energía potencial gravitatoria del cuerpo.
Trabajo y energía cinética
 |
Pero si la fuerza aplicada sirve solamente para aumentar la velocidad del objeto, entonces estás aumentando su energía cinética. ¿Qué relación hay entre el trabajo realizado por la fuerza y la energía cinética?
Fíjate en la demostración siguiente. Lo realmente importante es la conclusión que se alcanza, pero debes darte de cuenta de que se trata simplemente de relacionar adecuadamente expresiones que ya conoces.
A partir de las ecuaciones de la cinemática
vf = vo+ at x = xo + vot + ½ at2
puedes obtener que

siendo d=x-xo el espacio recorrido por el móvil, durante el cual se está aplicando la fuerza F.
Si tienes en cuenta la ley fundamental de la dinámica, F = ma , sustituyes la aceleración en la ecuación anterior y despejas el valor de F resulta que:
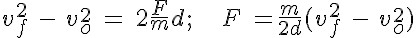
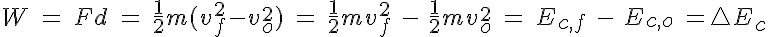
Por tanto, el
trabajo realizado por la fuerza sobre un cuerpo es igual a la variación de la
energía cinética que experimenta ese cuerpo.
Comunicando energía a un objeto
A un cuerpo de masa 5 kg que está en reposo le aplicas una fuerza horizontal constante de 100 N. ¿Qué velocidad lleva cuando ha recorrido 20 m?
Realiza el cálculo de dos formas: en primer lugar, teniendo en cuenta que el trabajo realizado por la fuerza sirve para aumentar su energía cinética, y, después, utilizando la segunda ley de la dinámica y las ecuaciones del MRUA.
 |
Trabajo de las fuerzas que se oponen al movimiento
Ahora vas a considerar las fuerzas de frenado y las de rozamiento, que se oponen al movimiento y hacen disminuir la velocidad de los móviles y su energía cinética.
¿Qué sucede con la energía perdida? En realidad no se pierde. Frótate las manos, apretándolas con intensidad. Para deslizar una contra otra tienes que vencer la fuerza de rozamiento entre ellas, de forma que el trabajo que realizas para conseguirlo se invierte en aumentar un tipo de energía que está relacionado con la temperatura y que se llama energía térmica.
Trabajo y energía
El trabajo que realiza una fuerza externa que actúa sobre un objeto sirve para aumentar su energía potencial, su energía cinética o ambas.
El trabajo de las fuerzas de rozamiento hace disminuir la energía mecánica del objeto. Esa energía perdida se transfiere en forma de calor entre los cuerpos implicados en el proceso, aumentando su energía térmica y su temperatura.
El trabajo y el calor son dos formas de transferir energía entre los cuerpos, modificando su energía.
Una frase para la historia
"La energía no se crea ni se destruye, solo se transforma"
Es otra forma de explicitar el principio de conservación de la energía: si un cuerpo gana energía es porque otro la pierde, transfiriéndose la energía de uno a otro en forma de trabajo o en forma de calor.
 |
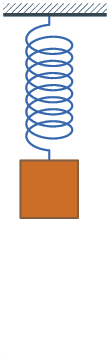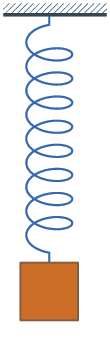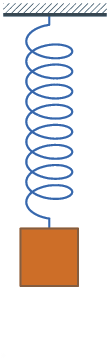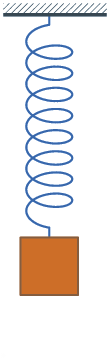 |
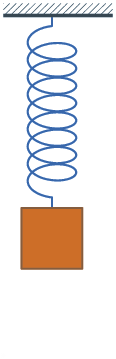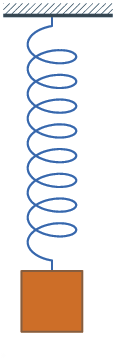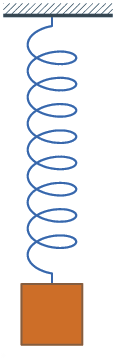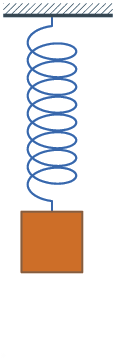
Transformaciones de energía en los muelles
Cuando una masa está unida a un muelle que oscila verticalmente, puedes observar que se producen transformaciones de las energías potenciales gravitatoria y elástica, además de la energía cinética.
Fíjate en que cuando el muelle está comprimido al máximo, la energía potencial gravitatoria y la potencial elástica son máximas y la cinética nula; cuando está estirado al máximo, la energía potencial gravitatoria es mínima, la potencial elástica máxima y la cinética nula; y cuando pasa por el punto intermedio, en el que el muelle tiene su longitud normal, la energía potencial gravitatoria es media, la elástica es nula y la cinética es máxima.
En el muelle de la derecha la oscilación se va amortiguando, por lo que hay pérdidas de energía que se transforman en calor, dando lugar a un aumento de la temperatura del sistema muelle-masa unida a él (como la pérdida de energía es muy pequeña, el aumento de temperatura es inapreciable).